0 前言
3D打印混凝土技术作为新兴技术,由于其不需要模板,节省大量劳动力和可打印复杂造型的特点,得到了大家的关注。但是,利用3D打印技术建造想要的结构,成型精度是必须考虑的一个问题。成型精度受材料性能、打印设备及打印工艺等的影响,本文研究了工艺参数对成型精度的影响。
3D打印混凝土过程中,需要设定的工艺参数有很多,例如进给速度、挤出速度、喷头内径、空走时间、分层厚度、搭接宽度、打印路径以及成型方向等。打印工艺参数是决定成型精度的关键因素,而且工艺参数设置值发生变化,打印成型精度、整体结构稳定性也会发生很大变化.
进给速度影响材料离开喷头时的初速度,对打印材料的挤出成型状态产生影响;挤出速度影响喷头单位时间内出料量的多少;分层厚度是产生台阶效应误差的主要因素;搭接宽度对打印构件的黏结性能产生影响;打印路径影响打印构件整体稳定性;供料速度影响挤出材料的密实度,进而影响打印成型精度。
本文从可控可测量的角度出发,参考国内外3D打印装置,在研制特定打印设备及打印材料的前提下,确定进给速度、挤出速度、分层厚度及搭接宽度为主要工艺参数,探究这四种参数对成型精度的影响规律。
1 分层厚度对成型精度的影响
分层厚度指打印喷头每走完一层的厚度,受打印材料特性(塑性、流变性等)影响,不同层厚条件下打印段产生的沉降变形也会不同。因此,分层厚度对打印构件最终的成型精度有重要影响。
1.1 试验方案设计
(1)确定打印装置和打印构件,见图1和图2。

(2)划分打印层厚度。设计构件高度180 mm,喷头内径20 mm,分层厚度值应当小于喷头内径,确定180 mm的三组公约数12 mm、15 mm和18 mm为分层厚度值,其对应打印层数分别为15层、12层和10层。
(3)确定打印路径,生成G代码。
(4)将G代码导入打印机完成实体打印,如图3所示。

1.2 试验结果及分析
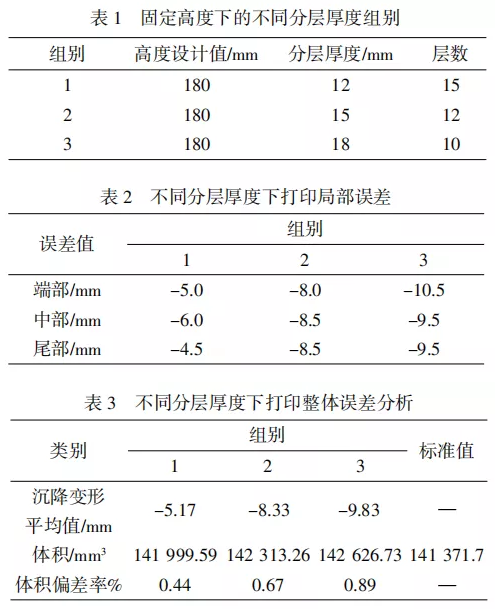
表1~表3为不同分层厚度下层高变形测量的误差分析结果。由表1和表3可知,在保证打印构件设计尺寸统一的前提下,分层厚度越小,构件成型的层高沉降变形越小,成型精度越高;分层厚度越小,构件体积偏差率越小,构件成型精度越高。
2 搭接宽度对成型精度的影响试验
搭接宽度是指并列挤出段之间的重叠部分。搭接宽度太大,会造成相邻挤出段之间堆叠隆起;堆叠宽度太小,则会造成相邻挤出段之间产生空隙,不能保证两段之间有效黏结,从而对构件的结构稳定性产生影响。喷头内径为20 mm时,设置搭接宽度分别为0、5 mm、10 mm、15 mm的打印试验,通过观测并列打印段的平整度,判断合适的搭接宽度。具体试验如图4所示。

由图4和测量数据可知:当搭接宽度为0时,打印段之间的空隙十分明显,不利于相邻打印段之间产生有效黏结,影响打印构件的整体稳定性,甚至发生剥落现象;当搭接宽度为10 mm、15 mm时,有较明显的隆起分层现象,打印构件表面精度较差;当搭接宽度为5 mm时,相邻打印段之间由于搭接引起的表面隆起误差在1 mm之内,打印构件成型表面无明显隆起和缝隙,表面精度高。
更换内径为15 mm和25 mm的喷头,重复上述试验,得出内径为15 mm时,表面成型精度最佳搭接宽度为3.5 mm;内径为25 mm时,表面成型精度最好,为6.5 mm。由喷头内径与搭接宽度比值关系可知,搭接宽度与喷头内径的比值约为1/4时,打印构件表面成型精度最好。
3 挤出速度和进给速度对成型精度的影响试验
3D打印将三维构件转化为二维数据继而生成数控系统所识别的G代码。挤出速度与进给速度在研发的极坐标3D打印混凝土装置中分别由G代码中的ΔA值与F值确定。两者与坐标变化值相关联,如果挤出速度大于进给速度,则挤出量大、喷头移动速度慢,打印线段的线宽会很大。如果挤出速度小于进给速度,则挤出量小、喷头移动速度快,打印线宽变小,甚至造成断丝现象。为此探究二者在不同情况下的匹配关系。
3.1 打印头仅发生旋转时ΔA与F的匹配关系
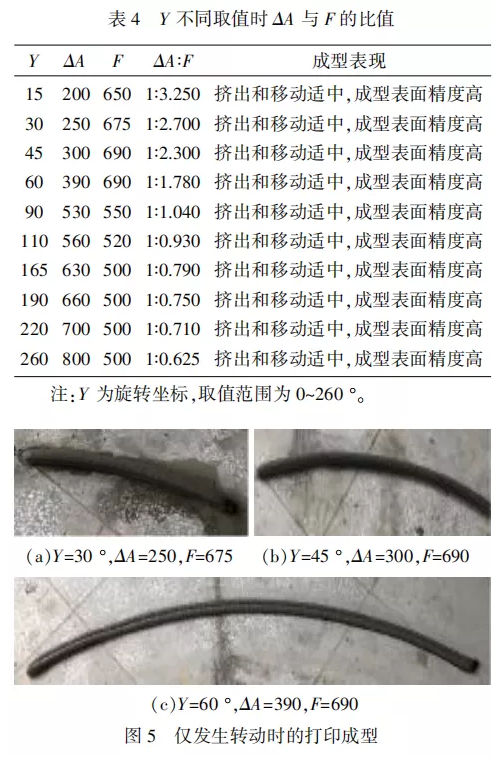
通过试验测得如表4所示的ΔA与F对应关系,拟合的函数关系式如下
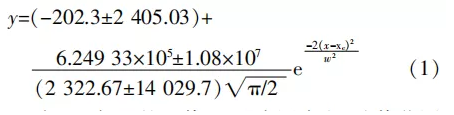
式中:y为ΔA与F的比值;xc无实际意义,取值范围是(394.360 6±147.064 1);w无实际意义,取值范围是(2 322.660 15±14 029.716 24)。
根据旋转坐标Y不同取值时ΔA与F的比值进行试验,得出图5所示的现象。从图5可以看出,此时的线条成型较好,成型的表面精度较高。

3.2 打印头仅发生径向运动时ΔA与F的关系
试验后,拟合的函数关系见式(2):
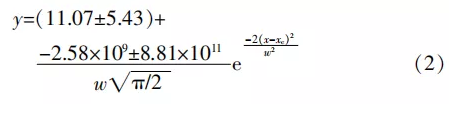
3.3 打印头同时发生旋转与径向运动时ΔA与F的关系
通常情况下,一段复杂打印段可通过切分成若干小段拼接的形式来定位打印路径的坐标点,当X、Y有一方相较于另一方值很大时,可将变化大的一方做主动因素,变化较小的为从动因素,根据前述仅发生旋转(X向)或仅发生径向(Y向)运动时的函数,依据主动因素规律确定ΔA与F的值。
当X、Y值变化差异不明显或不规律时,可根据挤出体积等于成型体积进行数学建模,利用单位时间内打印材料的挤出体积与打印成型体积相等的基本原理,见式(3):

式中:A为挤出速度,mm/min;F为进给速度,mm/min;S1为喷嘴截面积,mm2;S2为打印材料挤出后在工作台上成型的截面积,mm2。
打印材料被挤出瞬间,其形状与喷嘴形状大体相同,近似呈圆形,故其横截面面积Sa可以表示为式(4):

式中:R为喷嘴直径,mm;Sa为挤出材料的截面面积,mm2。
但在实际打印过程中,打印材料会受到上方喷嘴和下方打印工作台的约束,当材料逐层叠加时,打印材料会被挤压变形,变成近似矩形的横截面,那么这个矩形的近似截面面积见式(5):

式中:Sb为截面面积,mm2;d为挤出料线宽,mm;h为层厚,mm。
打印材料被挤出后在工作平台上形成的线宽d受到挤出速度、料斗内旋转叶片转速及供料速度等因素的影响。因此,必须建立d与各影响因素的定量关系式。研究多个变量之间的关系,需建立指标与多因素之间定量关系的回归分析方程,称为多元回归分析法,原则上均可转化为多元线性映射方程。将进给速度设为一定值,考察打印料斗内旋转叶片转速s和d之间的关系,假设二者之间存在一种特定的线性关系,建立多元线性映射方程d=m+qs+ω,ω~N(0,σ2)。其中,未知参数m、q和σ都不依赖于s,而ω是一种包含其余各因素的随机误差。采用试验的方法确定m、q的值,取若干不全相同的转速值si(i=1,2···n)做独立性试验,由数控软件生成的数控程序随不同的层厚会有不同的转速s,现在假设由si(i=1,2···n)得到的样本为(si,di)(i=1,2···n),则有di=m+qsi+ωi,且各个ωi相互独立,于是di~N(m+qsi,σ2)(i=1,2···n)。由d1,d2···dn的独立性可知其联合密度L见式(6):
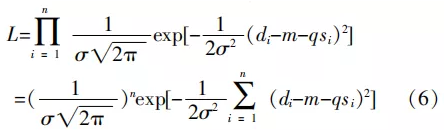
采用极大似然估计法估计未知参数m、q的值,即L取最大值,则式(6)右端中括弧中的平方和部分取最小值,令其关于m、q的偏导数等于0,可得到一个方程组,又因方程组中si的取值不全相同,系数行列式的值不为0,因此,方程组有唯一解,求解可得m、q的最大似然估计值。由此,便得到了在进给速度F固定的情况下d关于s的经验回归方程:d=m′+q′s,其中,m′ 和q′的值可以通过试验来确定, 联立上式,得到A和s的关系式,见式(7):

式中:A为挤出速度,mm/min;s为料斗内旋转叶片转速,s/圈;m′ 和q′是未知参数,通过试验来确定;h为层厚,mm;R为喷嘴直径,mm;F′为固定的进给速度,mm/min。
选择成型质量最好时挤出速度与进给速度的比值作为最佳比值,并将质量最好时的s′值代入经验回归方程并联立式(3)~式(5)得到式(8):

式中:A为挤出速度,mm/min;F为进给速度,mm/min;m′和q′是未知参数,通过试验来确定;h为层厚,mm;s′为成型质量最好时的叶片转速,s/圈。
联立式(7)和式(8),得到转速s和进给速度F的最佳匹配关系,见式(9):
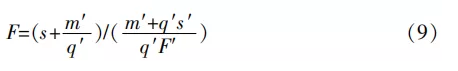
依据式(7)~式(9),由操控系统控制伺服电机确定打印料斗内旋转叶片转速s,理想转速值可由打印试验确定(本装置理想转速为0.9 s/圈),即可求出匹配的进给速度和挤出速度。
4 分层厚度差异的阶梯效应
4.1 外轮廓为斜直线下的阶梯效应
当设计构件表面轮廓为斜直线时,分层叠加打印技术导致打印构件边界处的误差可用△NFQ来表示,如图6所示。分层厚度越小,单个误差三角形也越小,通过数学建模的方式来表征实际打印中存在的阶梯效应误差。

假设构件总高度为H,在其截面△ABC中,AB与BC垂直,∠C为三角形坡度β,构件高度AB为h,构件的宽度BC为l,分层厚度为r,误差△NFQ的高度即层厚值为r,宽度值为q,则S△NFQ=rq/2。当分层厚度为r时,层数L=H/r 。因AB与BC垂直,构件总宽度l也被均分了L次,每层误差三角形的宽度值为q,则 q=l/L。由以上公式可推导出,当层数为L时,整个三角形截面产生的误差公式见式(10):

式中: S为误差。
由式(10)可知,误差面积只与构件高度H、分层厚度r、三角形坡度β有关,将式(10)作为控制阶梯效应误差的阈值函数。同样,当三维构件的外轮廓AB与BC不垂直时,可以将三角形分解成两个三角形分别计算,结果为两部分的和,见式(11):
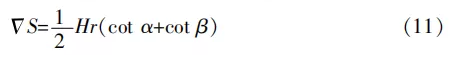
式中:α为∠A的度数。
4.2 外轮廓为弧线时的阶梯效应
图7为外轮廓面为弧线时的阶梯效应。由图7可知,当构件外轮廓表面为圆弧面[14]时,截面的每一层误差面积都不同。
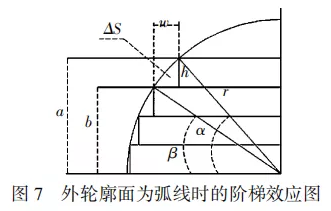
构件外轮廓为弧线时,误差面积计算如下:
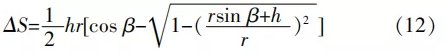
式中:ΔS为误差面积;h为层高;r为圆弧半径;β为三角形坡度,β∈(0,90 °)。
假设打印构件表面相对精度为θ(θ越小,表面精度越高),打印构件总高度为H,则可求得误差面积ΔS与表面相对精度θ的关系:θ=ΔS/H。假设打印构件的高度H=1 m,层高h分别为1.0 cm、2.0 cm、2.5 cm三种情况,打印构件经过分层叠加后的总高度H能够近似达到圆弧半径r,这样可将ΔS的表达式进行简化,带入θ的表达式中,得到式(13):
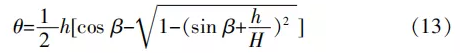
式中:θ为打印构件表面相对精度;β为三角形坡度;H为总高度,mm;h为层高,mm。
将h的值分别代入式(13),然后将θ关于β的函数关系式导入Origin 软件中,绘制不同层厚条件下表面精度与打印底角的误差函数图像,见图8。

分析任意一幅函数图像,层高h一定时,打印底角β越小,表面精度越高,随着β的增大,打印构件成型表面误差也越来越大。由此可得:在层厚一定的情况下,打印构件的底角越小,成型构件的表面精度越高。
将图8中三幅函数图像联立,当打印底角相同时,例如打印底角为π/4,层厚为1.0 cm、2.0 cm、2.5 cm时,对应的表面相对精度θ分别为0.006、0.025、0.035。再次验证前文关于分层厚度对成型精度影响试验的结论:保证其他条件不变的情况下,分层厚度越小,成型精度越高,随着层厚的增大,打印构件成型的表面误差也明显增大。
5 结论
(1)可打印的分层厚度会在一定范围内变化,但当分层厚度小时,成型精度高。
(2)当搭接宽度约为喷头内径的1/4时成型精度最好。
(3)挤出速度和进给速度的匹配关系作为影响成型精度的一个重要因素,需通过工艺试验确定。通过数学建模分析研究,阶梯效应误差可通过调整打印构件的分层厚度与打印底角进行控制。
(编辑:奚雅青)
延伸阅读:
装配式剪力墙结构预制率与成本的相关性分析 新型装配式钢节点混合框架结构及配套体系关键技术研究与应用 基于制造和装配的设计让预制装配式建筑的优势日益凸显(1) 凡本网注明“来源:预制建筑网”的所有资料版权均为预制建筑网独家所有,任何媒体、网站或个人在转载使用时必须注明来源“预制建筑网”,违反者本网将依法追究责任。 (2) 本网转载并注明其他来源的稿件,是本着为读者传递更多信息之目的,并不意味着赞同其观点或证实其内容的真实性,请读者仅作参考,并请自行核实相关内容。其他媒体、网站或个人从本网转载使用时,必须保留本网注明的稿件来源,禁止擅自篡改稿件来源,并自负版权等法律责任,违反者本网也将依法追究责任。 (3) 如本网转载稿涉及版权等问题,请作者一周内书面来函联系。
[责任编辑:Susan]